I STAND CORRECTED
For those of you who don't remember exact details about the movie Interstellar (2011), it mostly happens within a black hole system, composed of Gargantua - a 100 million solar masses supermassive black hole - Pantagruel, a main sequence solar-type star (G or F type) - and an unnamed neutron star.

Note that I had previously not read The Science of Interstellar by Kip Thorne before, which would have been of great help. So I wanna share of the aspects about Gargantua that was always a point of contempt for me, until very recently.
We know that for all the scientific realism and hard sci-fi the production of the movie incorporated into it, a lot of creative liberties were taken to make it more 'palatable' for the average viewer. Some examples of that is how far away Gargantua appears when observed from its closest blanet (yes with a B, we're dealing with black hole planets here), Miller's planet - in the movie it looks pretty far away, but in reality Miller's planet would be orbiting so close to the black hole that by some estimates it would only be about some tens to hundreds of kilometers above the ISCO, which is the inner edge of the luminous accretion disk. Which by itself, is only possible if Gargantua is a Kerr black hole with a rotational speed just 0.99999999999999 times the speed of light!
Of course that would be an absurd view in the sky, plus the various relativistic effects that should be taken into consideration when painting the sky - all that would have been overwhelming not only for the production but for the audience to take in as well. A similar case can be made for its waves, and the apparent color of the accretion disk, which had its blue/red shift color removed in the final rendering as to not confuse the audience, making it look a flat sun-like color.
So, given those and many other more subtle taken liberties, I thought to myself while parsing and reverse engineering the Gargantua system for myself - "oh wow, these planets must be absolutely toasted being this close to black hole!" BUT... I still had much to learn about it, it seems.
So here is a summarized version of what I initially thought of:
Gargantua is a sleeping giant, and it can't wake up
Gargantua's accretion disk is hot, but not really 'hot' compared to other black holes. Active black holes have accretion disk temperatures in the tens of thousands to hundreds of thousands of degrees, thus outshining even whole galaxies in the process of feeding. Those types of black holes are what we usually identify as radio galaxies or quasars - typically, a galaxy's central black hole in a feeding period. But since Gargantua's accretion disk isn't much hotter than the surface of the Sun, that is between 5700 and 6000 K, its disk is not only much cooler than usual, but also must be much thinner than usual? How thin? Basically non-existent! It is feeding basically on 1/3rd of the Moon's mass every year.
And even so, that means that at the distances involved between Gargantua and its blanets, that is, under 40 AU, the insolation for them is hundreds of times greater than Earth's because the accretion disk is thousands of times brighter than the Sun. That also happens with red giants, even though they are cooler than the Sun, their much larger surface area for emitting light makes them hundreds to thousands of times brighter. In this case, Gargantua's accretion disk is between 1.3 and 2.25 AU, roughly ~1.0 ASTRONOMICAL UNIT WIDE.
And if we tweak the feeding rate for the black hole until the thin-veil of gas around it isn't as luminous, we run into another problem: its Bondi radius - that is, its area of influence in interstellar space - is several parsecs wide, any unbound rock or cloud of gas can fall into it and add to the accretion disk mass, thus more than doubling its feeding rate and thus making it more hotter and brighter than it was before. In my view, it was one rogue asteroid away from just blasting the blanets with the wrath of 10,000 suns!
Before we continue, let's establish that 1.0 Earth insolation equals how much we get on average from our Sun, about 1360 W/m².
PHYSICS I OVERLOOKED
Turns out I was indeed correct in my assumptions, HOWEVER, it was incorrect to assume that the accretion disk is a perfect emitter from every angle. Which would simply not be true at all.
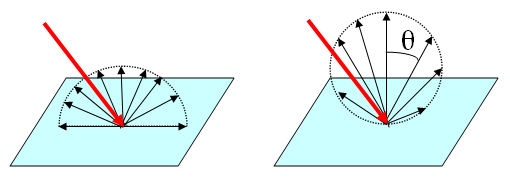
By considering the disk surface as a Lambertian surface, it means that an incident ray looks brighter or dimmer dependent on if the surface is face-on to the observer or at an angle to the observer.
Now let's imagine that our disk is a thin disk with a flat temperature profile, it would look very dim almost dark when observed edge-on compared to looking at it at 90° from the disk plane.

It is an okay assumption in this case, considering that when calculated for an accretion rate of 0.35 Moon-masses/yr, the disk temperature profile is more or less flat - between 5500 and 6000 K. We can then adopt an average solar-like temperature for our disk.

Our total luminosity based off disk geometry and temperature is about 70,000 Lsol, which is about 35,000 per face of the disk. Like I said before, putting an object even at 40 AU above either disk face means it is getting.... 35,000/40² = 21.88 Earth insolations (~30,000 W/m²). Which is not how it looks in the movie.
However, using Lambert's Cosine Law, we see that the insolation at our blanet is also dependent AND variable on its current angle from the disk's plane. In which case for simplicity, I will define the black hole system's Ecliptic the same as the accretion disk plane.
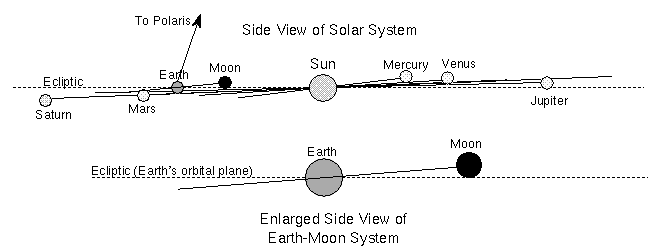
In our Solar System, the planets have formed more or less in this flat plane which we call the Invariable Plane, which is perpendicular to the Sun's rotational axis, turns out the Ecliptic is just another intersecting plane dictated by the Earth's orbit, which is convenient to us, because we then measure everything relative to it. Anyway, most planets and objects are within 7 degrees off that plane, and really at an average of 1.92° off it. If the planets around black holes are any similar to how planets form around stars, then that should also be somewhat true. Thus we should take the planet's orbital inclination in relation to the disk plane as a variable.
Inputting 1.50° as our maximum inclination at 40 AU we get only 2.62% of the disk face's maximum brightness, which is 0.57 Earth insolations or 780 W/m²! Way colder than receiving over 30,000 W/m². Usually that doesn't really come into play when dealing with stars because stars have well defined circular silhouettes no matter what angle you look at them from, so their perceived intensity is independent from viewing angle.
Now because our planet isn't always suspended 1.50° above the plane - it's relative vertical position changes throughout its orbit - that is the maximum insolation, the minimum will be a brief period where the disk occludes itself at inclination 0° which has nearly no power input for a non-lensed disk. Seasons will be mostly dependent on that relative altitude to the disk rather than orbit-shape dictated.
If we map out the disk perceived intensity by filling the environment with 'fog' which can reflect light back to the viewer, we would see a figure similar to this:

Basically two spotlight-like beams of light above and below the disk, with a very dark colder donut-shaped area around it, along the disk plane.
FROM EVERY ARTISTIC LIBERTY THEY TOOK, I'VE CHOSEN TO NITPICK THE ONE THING THEY GOT IT RIGHT FROM THE START, LMAO
Of course, this approach also ignores two factors that would be important in more realistic disks:
1. It ignores surface density, texture and layers.
The disk would present a 'thin' gaseous or plasma atmosphere above its surface, which would create a 'limb darkening' effect at shallow angles. That would decrease the amount of power received from the disk at a given angle by a measurable amount, because light rays would have to traverse more and more of this atmosphere and thus scatter along the way. This also means that even when observed edge-on, the disk wouldn't be truly dark, as the light scattered off the disk atmosphere above and below the faces would still reach the planet. Thus, the assumption of L~0.0 W/m² for θ~0.0° isn't true in the real world, because the luminous disk wouldn't be truly geometrically thin.
2. It ignores gravitational lensing.
The black hole would bend light from parts of the disk occluded by the black hole shadow, and parts above and below the disk, around the event horizon and towards the viewer. That would also add to the extra light received by the planet at any given position in its orbit, but mainly at that occlusion zone of θ~0.0°.
I'm yet to work those into my toy model.
Anyway I hope you've enjoyed the ride, this is another sneak peak into the DOMINION framework I'm building to help others into making well-researched space-focused sci-fi settings.
- M.O. Valent, 02/10/2025










