SCIENCE&ARTWORK | BINARY STAR SUNDIAL | PART 1

IS IT POSSIBLE TO CONSTRUCT A BINARY STAR's SUNDIAL?

WHY?

So this last week I've been trying to work on my own sundial to settle up an argument (with a flatearther, ugh), It works pretty nicely and got bit damaged by rain since it is made of paper, but my brief study of Gnomonics got me pretty interested in the craft as a whole, there are 'easy' and 'hard' ways to make sundials and solar calendars. You can scroll right to the end if you're not interested in the whole thought process behind its end design.

My first print of my gnomonic sundial, the lines are created by projecting a spherical grid onto a plane which is the dial plate. 

Anyone can use a base and a stick to simply mark the hours by the gnomon's shadow, but the instrument will only be able to tell hours. But to be able to tell the day and months/seasons, the designs and matemathics get a little bit more complex.

Fellas over the northern hemisphere might already be familiarized by the sundial design above, formed by a disk or dial plate, with a triangular gnomon on top of it. None of the shapes here are of arbitrary dimensions, the inclination angle of the gnonmon has to match your Latitude (North/South coordinate), and the size of the gnomon in relation to the plate will determine wether the instrument can only tell hours or include the seasons/month markings. For the northern hemisphere inhabitants, one can eyeball the inclination of the gnomon by pointing to Polaris, the North Star, whereas southern people have to use known landmarks and constellations to get a sense of where to point it.

If you look at my design, you will notice a straight line, and two opposing hyperbolae, the straight line is called the Line of Equinoxes, it is where the shadow of the gnonomon falls during the Autumn and Vernal equinox days (Equinox or Equinoctis meaning "equal nights") - the two opposing hyperbolae are the Solstice lines, where the shadow falls during the summer and winter soltices respectively, by marking intermediary hyperbolae one can mark the passsages of months and weeks through the solar cycle.

Because of the Earth's tilt, one can draft a simple grid like the one I did by constructing a spherical grid marked 23.5° north and south of the equator, then putting a light source at its center, then tilting said spherical grid to the user's latitude - the resulting projection onto a sheet of paper will be your markings, and the distance from the paper to the center of the sphere is the same from the plate to your gnomon's tip, which is what you can see I rendered in the 3D software, then printed.

Without a 3D grid (physical or virtual), it takes a lot of math to traditionally work out the specific lines you'll need for you sundial, that's why the ancients often cut the middle-man and just projected their sundials onto convex hemispheres and rings!

There is a whole bunch of other types of sundials each specific to what their projectionists wanted to be told by the sun as well, but do any of those work for a world with two suns?

THE SETTING

The system's stats I will be using thoughout this post

First of all, a quick googling of "Binary Star Sundial" retrieves not a lot of material, if someone has ever worked on anything like that, they didn't publish it on the internet, there are a couple posts on stackexchange and reddit dating back to 2016 but no solutions, most of them assume you can get away with a normal sundial since the shadows created onto a circumbinary planet would mostly be off by about 10° maximum - but this would only work as an approximation, depending on the specifics of the system, this would mean the clock could be offset by about 1h of the actual time (assuming the planet has 24h day/night cycle).

So before tackling the problem as a whole, let's see what changes from the traditional Terran sundial, so we can better know what challenges lie ahead:

DIFFERENCES BETWEEN SOLAR AND BISOLAR CLOCKS

1. MOVING SUNS

In the traditional solar clock, one can assume an inertial reference point, that could be either the static Earth with the Sun moving around it, or the static Sun-Earth system, with the Earth rotating around its axis.

On a bisolar clock, we have to consider not only either of those scenarios, but also that the suns are not static in the sky, they revolve around a common center of mass. Which means that for either scenario, the suns would always move significantly on a day to day basis - what would in itself, create a solar subcycle our natives to work with.

2. MISALIGNED ECLIPTIC

On Earth, the Ecliptic plane is the apparent path of the Sun across the sky throughout the year, it is pretty easy to follow through and it is what defines the constellations of the zodiac. On a circumbinary system however, one could either define the ecliptic as the planet's orbital plane, or the star's own orbital plane, in either case, both stars would constantly fall above and below the ecliptic as they orbit each other. Which means that the difference in orbital inclination between the stars and observer planet would change throughout the year as well. Anyone familiar with tracking the movements of Mercury and Venus in the sky will known how crazy the paths can look.

Because all of those movements are specific to the times and cycles at play, I will outline my process with an example so you can work out your own models of bisolar clocks. Since we cannot experience such a place, I will be using 3D software to simulate what it should look like based on the model stats given in my sketch.

UNDERSTANDING THE SKY

To keep things simple, I will work with geocentric coordinates, swapped the Sun in the solar system by a pair of twin stars with 80% of the mass, just so the brightness matches just the same on our planet, which had its tilt reduced to 20°. The star's also orbit each other at an angle of 5° from the planet's orbit.

Although for an external observer, the twin suns orbit each other every 36.1 days, the planet which is also orbiting the stars do not perceive this as being 36 Earth-days, we need to calculate the synodic period of the stars by using:

Which works out to be 41.25 Earth-days, or 990 hours, now we can use this information to set up the planet's rotation into some neat value that's easier to work with.

I will set the planet's rotational period to about 36 hours, this gives us a simple 10° per hour rotation, it approaches the solar subcycle to roughly 27.5 sidereal days (similar to a lunar month) - and makes the year about 192½ days. Meaning our stars move 13.1° over the course of a day, and half as much during daytime.

corrected suns declination at +0.624°

Usually, the planet's tropics would be located at latitudes 20° North and South of the Equator, but because the suns can gain about 0.62° of declination along their orbit, we can say that the tropics are found between 19° and 21° from the equator. This means that depending on the suns-planet alignment, the extra declination can come during solar opposition (suns seem aligned) or during maximum elongation (suns seem further apart).

The maximum elongation or separation between the suns in the sky would be about 14.5°, and this gives us another interesting alternative to measure the solar day, Mean Solar Time, which is measured from the barycenter, considered static while the suns orbit around it.

Further refinements put the sidereal day at 35h52m33s for a perfect 36 hour solar day

Let's also start our year in a point in the orbit when the suns seem further apart.

DESIGNING THE HOROLOGIUM BISOLARII

PRELIMINAR EXPERIMENT

An anallematic sundial consists of a vertical gnonom which marks the time throughout the day, but also tracks the months through the solar anallema by the length of the gnomon's shadow.

On Bisolaria, such an anallematic clock would produce two shadows which dance with twice the speed of the suns orbital period.

Each square is 10cm wide for scale, and the gnomon has 10cm from the base to the center of the sphere, the star light was tinted yellow and blue to differentiate, each time they switch sides corresponds to half a solar subcycle, and the whole animation takes place over two years (~385 sidereal days) on this planet, Bisolaria.

Each frame in the animation is taken at exact mean solar noon - if we picked a star to count solar days, then the frame of reference would wobble back&forth across all the four cardinal directions as that sun moves across the sky throughout the year, undesirable, which is why we count from the barycenter. Here we can also see the effects of the star's orbital inclination, at times a shadow appears longer than the other by a noticeable amount.

I bet we can use that tilt in the stellar orbital plane and the fact we are working with two shadows to come up with a creative horizontal anallematic clock and calendar. Why not double down with two gnomons then? My initial idea is to use two longer gnomons spaced in such a way that their shadows cross most of the time, the line at which they cross would determine the time of the year, while the point at which they cross would make up for the current hour of the day.

LOOKING AT THE SKY

So throughout the years, we would see the suns eclipse each other only during the planet's passage through the nodal line, where the sun plane crosses the ecliptic plane. We would also see the sun plane appear to tilt north or south as we cross the south and north pointing sides of the orbit, which by itself would be a good teller of seasons.

But we also have to consider the effects of the planet's orbital eccentricity, because the planet moves faster around the suns when it's closer than when it is farther - this causes the mean solar time to go faster and slower than the planet's true rotation period by a few minutes, which is what the Equation of Time is about.

I'm not mentally stable nor know math enough to digest the needed equations so I could explain them better, but I've found a couple tools online that will be useful in generating the data require to produce a clock for a fictional world:

• Analemma Calculator
• Sage Cell - Equation of Time

While the Analemma Calculator is pretty straightforward with single-sun systems, we'd need more work for the paths of the two or more suns we include. Below is a generalized version of the SageCell code, pointing where you need to input your data - if you're not familiar with Earth's parameters.

# Equation of time, by PM 2Ring - Generalized by M.O.Valent in 05/03/2023

d2r=pi/180

r2d=180/pi

    

dpy= [DAYS per YEAR]

mam=2*pi/dpy

oe= [AXIAL TILT in degrees] *d2r

sinOE=sin(oe)

cosOE=cos(oe)

ecc2=2*[ECCENTRICITY]

  

def eot(n):  

    a=mam*(n+10)

    b=a+ecc2*sin(mam*(n-2))

    c=(a-arctan2(tan(b),cosOE))/pi

    c-=int(0.5+c)

    return 720*c

def main():    

    P=plot(eot,0,dpy)

    show(P,gridlines=([0,5..dpy],[-20..20]),title="Equation  of Time",

         ticks=(30,5),axes_labels=("Day","Minutes"))

    

main()

By inputing 288.749d, 20°, and 0.01675, we get this graph:

Because the axial tilt and orbital period are similar to that of Earth's, we only see a small shift in the proportions of the EoT. By picking points along this curve, we can not only know the true time once the clock is done, but also construct the solar analemma ourselves. I've put certain points of the curve into desmos to solve as a sum of sine waves (some Fourier magic?) to approach a smoother useful form of it:

The Bayesian Adventures blog also offers a great tool for drawing the analemma and planning on its photography, it has a custom Octave code which you can use to accurately get the EoT and declination over time - but at this point I'm gonna stick to my fourier approximation of the EoT, and considering the start of the year at the Autumnal Equinox, it renders us the following shape:

The meeting of the loop would move up and down as we shift the autumnal equinox along the year, each point is the barycenter's position in 7-day intervals, the analemma is also slightly more elongated than the Earth's because I made the orbit slightly more eccentric

Meaning that over the course of a year, the barycenter can be about 12 minutes late or earlier than true mean time, this adds to our previous values for sunrise, which ends up making the suns rise/set up to 1h late or earlier than the barycenter, and 30mins on average.

To get the true position of the suns across the sky over the year we need to remember they move 13.01° in their orbit per day, so we can plot the sun's horizontal position in regard to the barycenter as the cosine of 13.1°xcurrent day (orange graph):

f(E,Dec); where E = EoT, Dec = Declination

We can then see how the sun orbits the barycenter, spiraling around the mean motion of the analemma, the other sun would be at the opposite side, with a relative 180° phase shift:

But to get the true spread of the suns around the barycenter analemma we still need to multiply that cosine function by its true elongation in minutes or divide the whole function so that both axes are in degrees - either works - we also need to add the sine of the 1.24 degrees of vertical component (actually half as much, or 0.62°) because that's how much our stars appear to tilt from the planet's perspective.

Then, here is the True Solar Analemma for both stars, X axis in minutes:

We can also add any angles (0-360) to that 180 se we change the phase angle of the stars in relation to the planet.

Meaning we could set that so the eclipses fall across a single line (like my first preliminary example), or across another curve give different phases. Since there only occurs 20 solar conjunctions in a year with the 21st marking the beginning of the next year, I'm sticking to putting those along the median line of the analemma. Because the eccentricity affects the planet speed around the suns, the number of days between each conjunction also changes if the planet is closer or farther from the stars.

 
Only conjunction intervals plotted, looks more Earth-like because the stars appear close

By looking carefully at which dates the stars align in this specific configuration, we get an average of 13.8357 sols!

Tropical setting sun (facing west) on Bisolaria, showing the analemma

EXPLORING THE ANALEMMA GRAPH FOR MONOLITHIC CALENDARS

Because of the differences in how the suns cross the sky in each region of the globe, each region would develop slight different.

By dividing the year in fourths (pieces of ~72 sols), we see that the Autumnal and Vernal equinoxes start with both suns or only one, respectively.

The Suns are apart from the barycenter by about 1.25°, giving a space between cast shadows of 2.5°.

So we can have a formation that allows for the identification of this event in all pieces of solar megaliths. But again, this is very specific to how we've set the suns phase angle of our day 0 of the year.

During the Northern Solstice (day 72), only one sun rises 0.9° short of 20° (so at 19.1° N), followed by the other sun at 20.9° N.

We can mark the shadow cast by the first lone sun with a larger rock than the rock illuminated by the second sun upon morning using a similar scheme to that of our equinoxial stone.

During the southern solstice we have a similar case, with a sun rising first on the inner 19° and the other rising above 20° S.

And so far, here is how our lithic calendar works for solstices:

With the Solstice and Equinox markings only, we get something that looks like this, scaled to a 12m-wide monument:

Solstice stones and autumn rocks spacings obtained by taking the sine of the angular spacing between stars (~2°) and multiplying by the distance radius

Based of this design (which I suspect is more adequate for the tropical zone), I've modeled and put it to the test in 3D, here are the results, within the first two hours of sunlight (less than 15° elevation):

For completeness, one can put a thin and tall stick on the other side to count days during sunset or sunrise, where the rocks end up pinched by the dual shadow of the post opposite to the equinox stone.

Example of a simple "T" shaped gnomon, during autumnal equinox, formed by a forked trunk and a branch:

CONCLUSION - NEGATIVE SPACE // CROSS SUNDIAL

After much fidling and playing with the illumination around my rock calendar and clock, the way out of this problem is to use what I call "negative space" sundial. A normal sundial uses the shadows of the sun cast by a gnomon to tell time - a negative space sundial uses the midpoint of the shadows cast by a gnomon to determine barycenter time.

In my initial experiments, I utilized a simple rod-like gnomon, which casts two shadows most of the time, by using two gnomons, the shadows cross at certain times - but not at all times, which would make it very hard to read the time by simply estimating where the shadows are supposed to meet in the midpoint.

sunlight angled 14.4° from each other, middle lamp indicates where the tip should point

I then experimented with one of the bowl or hemispherical designs to see how the shadows behave in order to fix this problem, adding a neutral light right in the middle of the two lights coming from the suns.

Seeing how this gnomon design (skeletal arrow tip above) makes the struts shadow cross at all times, I imagined that if the struts extended all the way to the other side, physically meeting at the nodal point of our hemispherical clock (center of the sphere) they would serve as tips/crosshairs. Simplifying the design makes it so you just need a bowl and two sticks perpendicular to each other.

Now, if you just put the two struts aligned north and south, you still have got the same problem, the north-south stick still casts two shadows, but something ✨MAGIC✨ happens by rotating the struts 45 degrees relative to North-South...

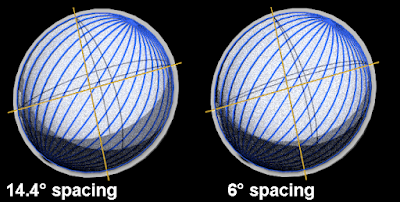
The struts project a little square window, whose north and south vertices are always centered!

it might not appear like it is centered, that is because the blue lines are physical protrusions which are slightly misaligned, as this was supposed to be placeholder

Each blue line is spaced 10 degrees and each frame moves 5 degrees, notice how the north and south crossings always cross the line at the same alignments, and this works for all sun angular separations - since the little window tightens into a diamond shape and then a line as the suns appear closer in the sky.

FINISHED BISOLAR DIALS

Hemispherical design, no need for complicated gnomonic projections

Simple horizontal design, gnomon has been tilted 45° and rotated 60° relative to north

Now that you have the solution in hands, have a good time working on your custom and over-elaborated clock designs, I'm eager to see how you all approach them - both in narration and technical specifications in the future!

AFTER QUESTIONS AND FEEDBACK I GOT FROM THE REDDIT COMMUNITY, THIS POST WILL BE GETTING A PART 2 (maybe 3?), STAY TUNED!

- M.O. Valent, early 09/03/2023

- M.O. Valent, edited 09/03/2023