TO THE TOP OF THE WORLD
When worldbuilding we are lead to add a couple of big mountains on the map and just call it a day - but, how tall should they be? *cue music*
That's a rather complicated question, to put it on simple terms, it mostly depends on the compressive strength and density of the material used on the mountain, and planet gravity.
The amount of weight above the mountain base shouldn't exceed the compressive strength of the material, ie, stress - or else the entire thing will collapse back to stability.
Let's assume our mountain is made of granite, which have a density of ~3g/cm³, and a compressive strength of 200MPa.
Let's make our mountain a cone of base h and radius r - it's volume will be given by:
The weight of our mountain can then be calculated by multiplying it's density, planet gravity and volume altogether.
So the little count below should give us the stress exerted by our mountain.
If something seems wrong to you, knowing that the Everest is 8,8km high, you're not alone - first of all, this model assumes uniform density, which let's be realist - don't really exist in most natural formations, because the Earth's crust exist in layers, which are twisted by geological processes over the eons.
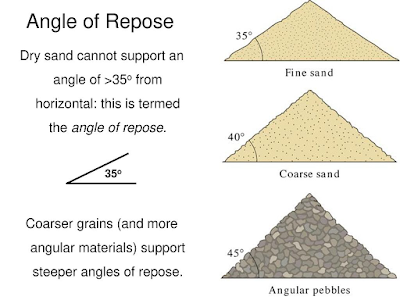
For any material that's being piled, there's a certain angle base-to-top up to which the pile is stable - the Repose Angle - which is defined by the specific material's static friction and grain-size.
Okay, knowing the angle of repose of our mountain helps us to better understand it's dimensions.
There are two ways to easily get to those values:
1. Figure out a way to find the exact materials in question, mix them, and then pour over a plane to a determined height or base width, and take the measurements yourself.
2. Take the data from someone that has gone through method 1.
On relatively small piles, we can assume dry grain size to be the most important factor, such as:
Although mountains are made of grains and crystallized material, it's much more cohesive than a pile of sand or muscovite clay.
Also, the grains within rock are compressed by their neighbors along the very vast majority of the rocky structure. So rather than considering grain size, we will be using static friction coefficients, and determine fault planes along which will form our mountain's slope - ie, an inclined plane problem.
Through a series of transformations, we get to this:
The angle (in degrees, not radians) at which a body/grain will roll downhill is equal to the inverse tangent of the static friction coefficient.
The problem here arises from the fact that it varies a lot from the materials used - you see, a piece of glass will slide more against concrete than a piece of rubber.
Concrete-to-Rock friction coefficients, depending whether it is wet or dry rock and what rock was tested varies from 0,50 to 0,70, with Concrete-to-Concrete friction having an average of 0,53.
With this in hand, our mountains can have slopes between 26,56º and 34,99º.
Now, we get to the though parts.
We know the angle of our slope, let's pick 32,47º, and determine that the base of our mountain is 16km wide, the crest of our mountain is at half that distance so 8km - to figure out the height, we just have to multiply the tangent of our angle by the base length (8km).
We get just about 5km, which, thrown into our stress equation, becomes 150MPa - which is little bellow our granite compressive strength limit, and so, just about okay.
I can't resist but to estimate things on Paart, so using the same constraints, this mountain could be 373m taller before having the same pressure at the base, implying a slope angle of 34,36º.
Calculating for a mountain that's just over the strength limit but with the apparent density of the Everest, we get about 9,5km tall, with a base width varying between 19,0 ~ 13,6km in radius depending on whether it's slope is less or more steep - compared to Everest's approximate 11,4km.
(relative to immediate surrounding terrain, measured from Everest Camp I at 6km to summit gives 3,7km, following the steepness to sealevel takes that to 11,4km).
Of course, mountains aren't just giant rocky cones that elevate above plains of terrain, mountains like the Everest originate from mountain ranges full of convoluted systems of canyons sculpted by the drainage of snow over the ages.
Be sure to give your world's top a couple of sister mountains that branch away into more and more along the entire mountain range.
Below a table of reference materials that you could use to make a mountain out of.
Theoretically, you could define the different layers of material in your planet's crust where the mountain forms, and then, calculate mountains within mountains for every material and thus determine what it's made of (relative to a cut at sealevel). But that's up to you now.