OTHER | SEEKING CREMATORIA-LIKE WORLDS | PART 1

CAN THE SUN BE A DEADLY LAZER?

Alright, let's establish some objectives with the rush of ideas, we want a planet that:

Is somewhat habitable, but only if lighting conditions are just right, that is - it has an overilluminated side and a dark side. In which case, life would need to move or cover itself when the surface passes through the overilluminated side, and do its thing when it is dark until day comes again. Like Crematoria from Chronicles of Riddick.

We will explore different scenarios in which that world might exist, and rank the possibilities from Natural / Realistic down to Designed.

One first idea that came to mind was to add more stars to the system, and organize them in such a way as to cause the desired effect... Can it be done?

RECAP ON DOUBLE STAR SYSTEMS

The illustration above sums up a simple case and a generalization of the conditions in which protoplanetary disks form in binary systems. Here we see that circumbinary disks occur only when the orbital separation is around 3-ish AU or less, and we don't see any disks around either star up to at least 50 AU separation between them - this occurs because given eccentricity of the system, no sufficient mass might be able to clump into a protoplanetary disk either because the stars scattered it all around a circunstellar cloud / off-system, or because all of the mass was consumed by the developing binary. Once distances are sufficiently large is that we start to see disks around either or both stars.

Such observations of primitive star systems tell us for example, that we shouldn't expect any planets around Alpha Centauri A or B stars, but on Proxima Centauri - which checks out so far as our telescopes are able to detect.

The dimensions of the protoplanetary or circumbinary disk in our binary system is quite important so we know what constraints the natural formation of planets and asteroid belts in our system.

As a general rule, the inner radius of the circumbinary disk is roughly 2 ~ 3 times that of the orbital seperation between the stars, and depending on the actual mass ration between the stars, a debris belt might be present in the inner system from material that was unnable to accrete into planets. BUT WATCH FOR THE MASS AND SEPARATION.

The example above highlights the need to give attention to either orbital separation or mass of the binaries in question. The case presented ends up being a sterile gas giant system because the star configuration pushes the stability zone way past the snow line of the binary (~1.2 AU).

This system can be made much more friendly to Earth-like planets or moons if the stars have greater mass, and thus more luminous output towards planets so far away. Or conserving the stars but increasing their orbital separation until we get a system around either or both stars, in which case it would be over 100~1000 AU wide.

It is possible to have both P-type and S-type planets in those intermediate distances, as long as the systems are relatively packed.

For an eccentricity of 0.2, the following is a good approximation for the outer limit of the star's planetary system:

Which results in larger limits the smaller the companion is, since its gravitational effect diminishes with mass, and the larger is the mass difference between stars, the more circular are the planets orbits around them. The planet's orbital eccentricity gets higher the more eccentric and similar are the parent stars, tending towards 1/3rd the eccentricity value of the parents as it approaches 0.5. So we would expect that the planets around our previous example to have a eccentricities of less than 0.06, which is actually more circular than the Moon's orbit around the Earth.

Given the luminosity of the stars in the example is 0.37 solar luminosities, if we want a planet on the circunstellar habitable zone at 0.6 AU with 2 AU to spare, then we have to space the stars such as that the Dsk_outer/separation value is equal to some 3 AU in this case, which ends up being 8% of the total separation by proportion, since both stars have the same mass. This gives us a minimum separation of 37 AU! If we get more conservative with the room to spare part, we easily arrive at separations far above 50 AU, which is confirmed while looking at binaries in space.

As for how far can circumbinary (P-type) planets orbit the binary, we can only estimate based on some real-life examples. COCONUTS-2b orbits its parent at distance of 6,000-7,000 AU, but remember that its system lies in deep interstellar space and might be easily disrupted by future star flybys. Given the mass of 6.3 Jupiters for the planet, and 0.37 solar masses (typical of cited M3 stars), the gravitational pull is close to 540,000 teranewtons, using F = GMm/R².

Referring to that value of 540,000 teranewtons as close to an upper limit, then the maximum distance we can put a similar planet around our binary pair is around to 14,100 AU. While the minimum distance would be above 3x the orbital separation, or greater than 110 AU, sadly too far into the depths of space for any life, but a P-type planet nonetheless. The vast distances involved for allowing P-type planets are also why they are such a rare find in nature.

Now that we've recollected everything essential into configurating such systems, let's talk about...

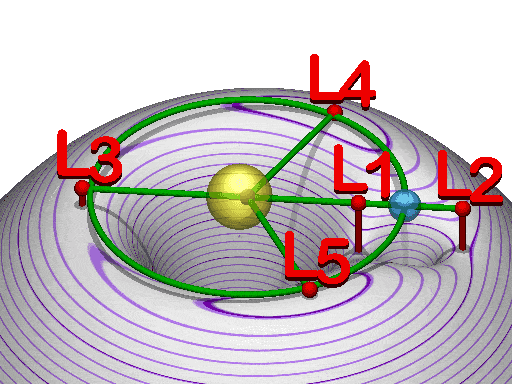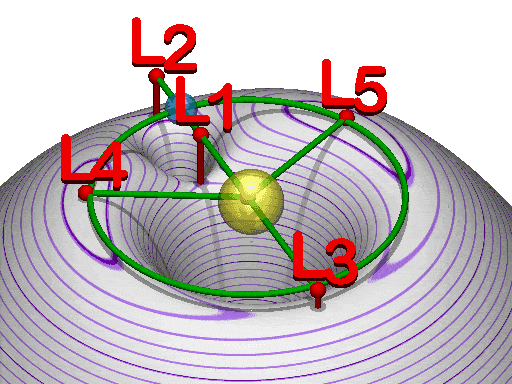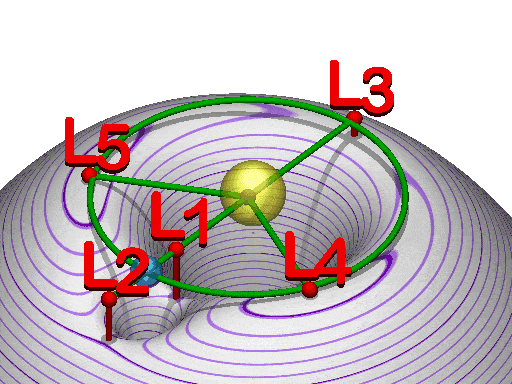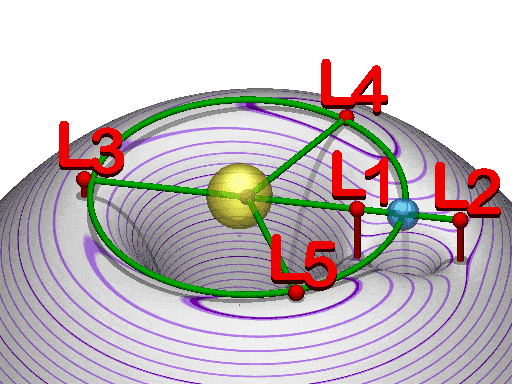
LAGRANGE POINTS

They are equipotential regions of space, where both the parent and satellite mass exert similar amounts of force over. 

These Lagrangian points exist between the two bodies at L1, opposite to the satellite at L2, opposite to the parent at L3, leading the orbit at L4 and trailing the orbit at L5.

In the solar system, the most notable lagrangian objects are the Trojan asteroids, which lie in the L4 and L5 points of the Sun-Jupiter system.

Now, because the "size" or "strength" of the Lagrange point is dependant on the system size and mass, the greater the mass we can shove into those points and get away with a stable system.

We have to note here that due the distances involved, the points L1, L2, and L3 are all too unstable for significant stay of any bodies, which is why we use them as gateways / low-effort insertion points for spacecraft, as you can quite easily travel through them. Points L4 and L5 are more forgiving for stability and degree of precision needed to hang around.

Going over planetary masses and doing a bit of equation balance, we find out that equation is only satisfied if the mass disparity for the primary body is gigantic, that is, if it holds 96% or more of the system's mass, which leaves us with 4% of the primary body mass to distribute amongst our satellite and Trojan-like body.

Back to the Sun-Jupiter system, the Sun being 1040x the mass of Jupiter - it easily comports at least another Jupiter-mass object at either lagrange points because of how extreme is the mass difference. Though such extreme cases are unlikely in nature, because of the way planets form and disturb nearby material during the formation process, hence why we have some asteroids with negligible mass as trojans, not whole planets.

T-TYPE  for 'TROJAN' PLANETS

For this to work out, we'd need a brown dwarf if our primary star is Sun-like, in which case, that brown-dwarf doesn't play a large role in illuminating the planet at all. If we want the secondary star be at least a red dwarf, then the primary star would need to be B7 blue giant star - that is also bad for us because blue stars are extremely short lived, just shy of 60-100 million years, enough to develop a primordial planet but no native life.

Say we want this system to live at least some 4.5 billion years, then our primary options are stars with up to 1.2 solar masses. That leaves us with up to 0.048 solar masses for a high-mass brown dwarf, low-key an actual flaring red dwarf (L0 or M9 type), with 1/1000th of the Sun's luminosity.

Located at either the L4 or L5 points of a double star system, such planets would have both suns fixed in the sky always at 60° apart, under the right conditions it is day in 2/3rds of the planet's surface at any point, and only truly night on the other 1/3rd.

But can we make it work? Uhhh... Kinda

My rendering of such hypothetical scenario, illumination is not realistic for viewing purposes

APPROACH 1: USE BROWN DWARFS

In this case, we give the planet a very slow rotational period, like +100 hours, this makes the planet have a very inefficient heat distribution, as when the night side turns back to the day side it had time to irradiate most of its energy. This is attainable in a three ways; the planet the is the tidally locked satellite of a gas giant, this way the orbital period of 4-ish days is the same as it's rotational period; or the planet has lots of moons, which slow the planet down over time; or the planet was struck in the deep past by another smaller planet, thus counter-acting its rotational momentum, or even, it has a slow retrograde rotation like Venus because of it.

We can also make this planet relatively small, so its volcanism and mass doens't make it retain a thick atmosphere, which would make this site unbearable due greenhouse effect.

And then we position such planet bit closer than what the habitable zone says it's safe, like 0.80 ~ 0.90x that distance.

The result is a world that gets near 1.5x as much sunlight as Earth (from the main star), but the thin atmosphere and amount of solar exposure would certainly be deadly to many known organisms. It might sound like a lot, given the Earth hasn't always had UV protection with ozone, but let's consider that the Earth's atmosphere has also been thicker in the deep past, but due atmospheric escape and gases becoming trapped in rocks, it has been getting thinner over time, which not only would have granted that Earth did not freeze in the Sun's early days as a main-sequence star, but also makes the planet habitable under the amount of sunlight we currently receive.

With a world getting that much sunlight from the start and having a thinner atmosphere with a slower or non-existent rock recycling process, we maximize the amount of radiation we can possibly get on the surface. The presence of liquid water on the surface also changes our outcome, since oceans are good heatsinks, the less water we get, the hotter it gets during the day, the colder are the nights. So we're looking for an alien world with a thin atmosphere and little to no water. This sounds pretty much in-line the large rocky moon of a gas giant in the habitable zone.

How large is this gas giant? Well, we cannot get away James Cameron style, with a small gas giant and it's unbelievably large moon. Gas planets are on average 10,000 to 40,000 times heavier than their moons, which means that a gas giant with an Earth-mass moon would need to be on the order of 4,000 to 40,000 Earth-masses, or at least 15 Jupiter masses. Even Saturn is 4,750x heavier than its largest moon, Titan - but for really large moons we have to get into the realm of Brown Dwarfs.

The brown dwarf aspect of the system also helps us to add more heat into the system, in which case, you wouldn't want to be under either the suns or the brown dwarf in the sky.

I suggest you too google the chosen names, cool trivia

Hekate, our moon of a trojan planet gets about 1.41x times our solar irradiation from its parent star - however, since it is only at 4 million km from its host brown dwarf, it finds itself tidally locked, receiving 1.41x times the energy we get from the sun, but most of it is in the form of infrared radiation instead of visible light and UV rays. So while the illumination of the planet is similar to that of Earth's, its infrared irradiation is nearly 4 times that received by the Earth.

The orbital period of Hekate is also about 11 days and 4 hours, which makes for 5 and half days in hot darkness, and 5 and half days in bright hotness.

The brown dwarf appears larger than the star in the sky, and would be its primary heat source.

The problems with this solution are:

1. Brown Dwarfs cool down over time. In this configuration, the system would only be overwhelmed with heat for the first few hundreds of million years after the system's formation, the brown dwarf would have cooled to a mostly inoffensive heat source at 500 K after 1 billion years, needless to say, the planet would be much more hospitable to life when older than that.
2. The planet rotation slows down over time. So we might get some "run away from the heat" action when the planet is primitive and young. But if the world is more mature, then the brown dwarf stays fixed in the sky as the planet tidally locks to it.
3. Extra heat is not the extra radition we're looking for. Of course, we want things to burn in the light of our evil star, but the extra heat is going to get distributed across the planet as the atmosphere spins, making such worlds a Venusian/Wet-Venusian by default.

How one experiences day and night cycles while tidally locked to a brown dwarf

Many bright stars hold companions which are much less luminous than themselves, it is harder to detect those around large bright stars than it is around dimmer less massive stars because of the greater effects of gravitational wobbling, hence the biases in data towards companions of large stars being generally heavy stellar remnants.

This type of system might actually exist in enough abundance as to cover several thousands of systems in the whole galaxy, for all single bright sun-like stars that's 110 candidates per 1000 stars. Even if the chances of this arrangement are 0.1% within this population, we're still looking at some 45 million systems across the Milky Way galaxy.

APPROACH 2: USE MORE STARS

We've previously calculated that even for a decently sized brown dwarf, our main star would have to be larger, and thus bluer, more luminous, and short-lived. So to circunvent this mass problem, we will not inflate a single star, but instead are more smaller stars as a center of mass.

My first example presented two 0.75 solar-mass stars, which amount to 1.5 solar masses, yet, the system is going to live for 25 billion years, and it is only 2/3rds as luminous as our Sun. Can we get away with that kind of arrangement? With that specific one, no, for already specified reasons that is rather very unlikely for planets to form that close to the binary pair as it is.

A modified version using near-solar mass twin stars for a total of 1.88 Msol would push the habitable zone outwards to a minimum distance where planets can form in stable orbits around binaries. Now, because of the distances involved, since the two main stars are so close together and far away from where we want our trojan planet, we will treat them as a single massive object with near double the mass of our Sun, pushing our 4% mass to work with up to 0.075 solar masses, which is inside the realm of red dwarfs even if we take a bit to feed a trojan brown dwarf. Interesting...

If we pack two sun-like stars 0.15 AU apart, then the next safest stable distance for another body would be around 2~3x that distance, at about 0.40 AU, where we could, put another star... or another pair of stars!

What I find interesting in this scenario is that we can get multiple eclipses in a row, or even, a multi-eclipse, because at certain astronomical alignments, more than 1 star can be eclipsed at once if the planet and star postions are just right.

Here is an attempt at showing how the eclipse shadows move as the stars move, notice that the planet zips by multiple shadows at once, the star's orbital plane is inclined 2.72 degrees from the brown dwarf's orbital plane.

You can make an animation like the previous one that by setting up a curve screen about the radius of your planet's/moon's orbit and let the sunlight projects shadows on it. In my case the whole thing spins because I've animated the whole orrery for accuracy.

I find the eclipse scenario quite enticing, as it poses a short window of safe surface activities before everyone needs to cover from intense sunlight. But here are some problems:

1. There isn't enough shadow time. The transit of a single eclipse under this configuration is ~13 hours, under the right conditons of inclination, the planet might experience a total of ~52 hours or ~2 days of eclipse per orbit, but typically over the year, the eclipses are far too spaced out, or if the shadows overlay we get darker but same-duration eclipses (assuming zero orbital inclination between planet and brown dwarf). Plus, the eclipses only happen across an arc that's 22.5° across the planet's orbit on the night-side of the brown dwarf, due the orbital separation of the stars and distance to this planet, that is only.
2. The lighting isn't radical enough. At a distance of 1.7 AU, the planet receives a collective 1.11x the solar constant from the parent stars, and an extra 0.92x all in infrared from the brown dwarf, to which it is likely tidally locked, the planet is also very likely to be a Venusian world.

The typical mass ratio in binary systems is 3:1, followed by 2:1 and 5:4, which sounds concerning at first. However, when in a multiple-star system, the tendency is for stars to settle with similar masses as opposed to unequal masses, followed then by a 3:2 ratio. So for this configuration, this system is not at all strange, however, our trojan scenario will be always a subset of those quadruple systems with equal mass, so we can confidently say that it is considerably less than 2 per 1000 stars, or about <<1 billion quadruple systems sporting sun-like components. We'd need to know how many of those systems have planets around them to narrow our subset, given we know at least 200 quadruple systems, from which we know only two that have planets (30 Ari, and Kepler-64 b), the chances drops down to about << 1% of those, that is a small subset of the less than 8 million quadruple systems with planets galaxy-wide. Pretty unlikely to occur in this exact configuration, though we get a lot of near-misses.

But not gonna lie, the dance of multiple stars is pretty hypnotizing to watch from a moving frame of reference...

IN THE NEXT POSTS WE EXPLORE OTHER WAYS TO MAKE CREMATORIA REAL

• S-type planets in close binaries
• Dying binaries
• Luminous black holes

- M. O. Valent, 05/02/2023