BUILDING BLOCKS | PART 6 | KEPLERIAN DISTRIBUTION

KEPLERIAN DISTRIBUTION...

And I well thought I wouldn't come back to the BUILDING BLOCKS section, ha, I was pretty wrong I guess.

SO, last time we scratched a talk about placing planets in their orbits (PART 4), we saw what I now call 'Keplerian Distribution', in short, you set a base number, usually 0, and build up a progressive sequence with some sum or subtraction over it, and there are your planetary orbits.

If we take a look at our solar system, we will notice how planets are spaced.

Mercury - 0,38 AU

Venus - 0,73 AU

Earth - 1,00 AU 

Mars - 1,52 AU 

Jupiter - 5,2 AU

Saturn - 9,5 AU

- -

Johannes Kepler when measuring the Solar System, noticed that if we begin a sequence at 0, 3, 6, 12, 24, 48, 96... and so on, added 4 and divided by 10.

4, 7, 10, 16, 28, 52, 100... /10  =  0,4 AU, 0,7 AU, 1 AU, 1,6 AU, 2,8 AU, 5,2 AU, 10 AU...

Of course this kinda works well because stable orbits form from orbital resonances, and those really have a progressive mathematical relationship.

The original Keplerian Distribution falls like:

 A = ([0, 3, 6...] + 4) / 10

Repeat the procedure for every planet you have to put in place.

Keep in mind that although I stated C is any given value between 0 and 10, that is not quite a rule, but also, your orbits that fall outside the outer boundary of a star system (forty times the host star mass in AU) must be excluded if so.

I've made a Keplerian Distribution Graph in case you having any problems in visualizing what's going on.

- M.O. Valent, 28/06/2019

OTHER CONCEPTS | SUNSETS

S U N S E T S

HEY! VSAUCE HaSFi! Valent here...

Ever sat at an open field or beach, to watch the sun set?

If no, you should probably do it someday, well I love watching the sunset, not only because I like seeing the stars and satellite constellations fade in, but also, because the sky changes its color as well the sun does...

Sky color...

Rayleigh Scattering is responsible for making our skies and blue eyes BLUE, shorter wavelengths like violet and blue gets scattered more in the particles that make blue eyes and air than longer wavelengths like yellow and red.

Except when during the sunset, there is way more air in the way, so all the blue light coming from the sun scatters in the way, and only the yellows and red photons manage to go practically straight through towards your retina... We see a orange/reddish sun setting...

You can also observe this phenomenon while in pretty polluted urban areas, when the pollution makes the air so dense, that you can actually the see the golden disk of the sun through the smog.

The atmosphere thickness is roughly 100km, being that most of it (97~99%) is concentrated in less than 30km high, during noon you can see the blue sky and an overall white/yellowish sun.

When the sun is setting, there is around 639km of atmosphere in the way, making it reddish, and for that, since yellow/red light are ~45% the visible spectrum, we can assume this much atmosphere is gradually responsible for "absorbing" ~65% of the incoming sunlight, we will come back to this later.

If we make the atmosphere thicker, twice as thick for instance, during noon the sun will appear yellow as during 9h and 15h because of those extra ~30km in the way. As such, during sunset or sunrise, there will be ~816,5km, in this case absorbing up to 83% of the visible spectrum, letting only red and deep red pass by.

Now remember when I said that the atmosphere "absorbs" blue light in the path during sunset?

We can plot how much air is needed for the sun to appear a certain color, this will give us some idea of what is going on.

Okay, so, for an Earth-sized planet and an Earthly atmosphere, we have:

Atmosphere height = 32km (99% atmospheric mass)

50% of AT.mass is located within 5,5km from ground.

40% of AT.mass is located between 5,5km and 18km from ground.

9% is located between 18km and 32km from ground.

1% is spread up 600km high (ignore it)

Then we notice that:

50% AT.mass occupies only 17% of the AT.volume.

40% AT.mass occupies another 54% of the AT.volume.

10% AT.mass is spread across the rest 28% of AT.volume.

And this proportions are valid for any direction you look at in an earth-like atmosphere.

Let's face the atmosphere density as those 3 phases, any direction we look at will pass through these 3 phases, but in different scales, unless you are in higher altitudes, but we are counting for an observer at sea level.

Now, for Earth we have 639,28km of air in the way during sunset, which is ~19,97x thicker than the atmosphere at zenith.

Using triangles and the horizon drop to determine at what distance each phase of atmosphere ends, we see that the phases maintain their proportion, like we said before.

50% of the air in the way stands up only in the first 110km, the other 40% are up to 458km and etc.

 

110km is 20x thicker than 5,5km, hence, we have 20x more absorbency than at noon, we find that at noon, atmosphere filters 3,25% the visible spectrum starting from violet.

If the sun is 45º high, the atmosphere in its direction is 14,14x thicker so its absorbency is 14x than at n--

NOOOO NONONO! Am gonna stop you right there!

See, when we draw our triangle being 32km high (atmosphere height) and 45º in one side, we get our hypotenuse 452,5km long, the path of light is 14x greater than at zenith, BUT when we look at our phase boundaries, they've only grown up by 40%, then the real absorbency is 1,4x the zenith's.

At sunset/sunrise and noon are the only valid straight up values that are true, for any other direction you must divide the hypotenuse length by the atmosphere height which happens to be the opposite side of the triangle.

Now, how do I calculate this for a different planet?

We will need to calculate chords...

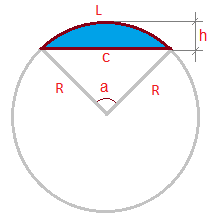
On the picture:

L - arc length

h- height

c- chord

R- radius

a- angle in degrees

But, let's consider 3 things first:

1. We know the radius of our planet (Rp), and we know the height of our atmosphere at the zenith (hA).

2. We know the radius of our atmosphere. (RA= Rp + hA)

3. Height of our chord shouldn't be higher than hA.

Now, let's say our planet is 5.000km radii, and it's atmosphere is 52km high (sun-like star):

Rp = 5.000 km

hA = 52 km

RA = 5.052 km

c = 2 * [ RA * sin( a / 2 ) ]

c = 2 * [ 5.052 * sin( 16,458 / 2 ) ] = 1.446.18 km

Since we can only look one direction at the time (duh) we just need half this segment for our maths... So our useful c' is 723km.

h = RA * [ 1 - cos( 16,456 / 2 )]

h = 5.052 * [ 1 - cos( 16,456 / 2 )]

h = 52,00 km.

For Earth the angle a just happens to be 11,463º.

Okay, so 723km are 13,9x thicker than 52km, and 52km is 1,625x thicker than 32km.

1,625 * 3,25% = 5,28%, is how much light is scattered away during this planet's noon.

13,9 * 5,28% = 73,392%, is how much light is scattered away during this planet's sunset/sunrise.

I will someday find out a real formula for that which will pop the exact ratio of atmosphere in the way, but for now, we have a Desmos graph, and even so, my abilities with it are pretty limited...

This graph is configured for Earth, and I recommend you to have a protractor in hand while calculating your angles... 

[VAL'S ATMOSPHERE THICKNESS GRAPH]

Here is how it works:

Line Code:

Green - Earth's surface

Blue - 5,5km high (Lower Troposphere)

Purple - 18km high (Lower Stratosphere)

Black - 32km high (Stratosphere)

Red - Viewing path

Variables:

c - Any value between 0 and -10 will give an angle between 0º and 90º up. Tweak in between 0 and -1 for angles up to 45º. Check your angle by aligning the protractor with the graph's origin.

r - Planet radius.

b - height of the graph, set it to minus r so your planet surface lies on the origin.

To obtain the atmospheric layers radius, divide it's height* by the planet radii, then subtract it from 1,0. Set the numeric variable in the graphs with the resulting number.

*calculate the heights with the proportions previously stated.

Since your observing point is the origin (0,0), the intersection point between the red line and any atmospheric layer coordinates gives your triangle sides, where the X coord. is the base, and the  Y coord. is the opposite side. Square them up and root the hypotenuse up to get the path.

If your line pass through the (14.4 , 2.4) coordinates (Lower Troposphere), your triangle is 2,4²+14,4² = 14,59². 14,59km is 2,65x 5,5km, then, by looking 9,46º the atmosphere visible light absorbency is 2,65x that of noon.

You can follow like that and so on.

Bye.

- M. O. Valent, 25/06/2019

OTHER CONCEPTS | SUNLIGHT

S U N L I G H T

Ever wondered if the distance between Earth and the Sun is the true cause of seasons?

Well, many may already know that the statement above is FALSE... Up to a point...

The cause of seasons big player is the Earth's axial tilt, however, it adds up that global temperature change is influenced by that 3.3% change in sunlight irradiation of our blue marble(+3,3% january / -3,3% july).

In terms of energy, sunlight at Earth's surface is around 52 to 55 percent infrared (above 700 nm), 42 to 43 percent visible (400 to 700 nm), and 3 to 5 percent ultraviolet (below 400 nm). At the top of the atmosphere, sunlight is about 30% more intense, having about 8% ultraviolet (UV), with most of the extra UV consisting of biologically damaging short-wave ultraviolet.

 This image is 1000px wide and ports the approximate proportion of sunlight output

Now, this can play a hella big role on starbuilding, here is why:

The peak emission our star is around green light, as far as we know our plants and other photo-synthetic life reflects those peak wavelengths for protection from overexposure to high-energy light.

Since humans and other species are quite more sensible to green tones, not only due to our environmental agents like camouflage of harmful snakes and insects, but due to a greater potential of acquiring visual data.

If your ambient light is reddish, it makes more sense that animals would learn to differ more shades of red than other non-existent colors like blue.

Now pack that to a larger scale, and we will see that almost all alien species with eyes that are similarly to ours, which developed within fairly different sunlight color and environmental biology, will have a certain degree of red/blue shifted Daltonism.

Picture a Kardashev II civilization arriving at a human settlement in huge dark ships with red lights all over its inferior hull, but despite that bad connotation red and black together have for the overall human population, their intent is purely pacific and their use of that look is just the way they were conceived to see near infrared light, making the ship visibly dark, makes it kind of gray-white to infrared light, which also explains the red lights under the hull, the same way it wouldn't make sense to use far UV in our car lights, aliens that see infrared wouldn't se any sense in using green or blues which are probably invisible to their biology born around a red dwarf/giant star emitting near infrared peaks.

It is also interesting to see how species born to see a certain degree of UV wouldn't be a good ground trooper in any interplanetary wars, since UV light scatter more in the atmosphere in ways that the air looks always foggy, reducing visibility down to a few hundred meters, their civilization might also use a lot of visible light in their communication technology, the same way we use Bluetooth and radio wavelengths.

We can define if our star emits decent amounts of ultraviolet and visible light and define its overall brightness.

Use a blackbody calculator to range your emission model.

Configurations:

Temperature = Temp. of your star, above choose Kelvin, Fahrenheit or Celsius scale.

Emissivity = Lum. of your star.

Wavelength = Insert a given wavelength and it outputs Spectral Radiance on the side box.

Lower Limit = 0,1 µm (shows most of ultraviolet)

Upper Limit = 3~5  µm (shows most of infrared)

Press CALCULATE.

For Vol, we have that the peak emission occurs at 493nm which is roughly this COLOR, while our Sun peaks at 500nm which is ~ this COLOR.

Sun model BLACK line; Vol model RED line

By tweaking the LOWER and UPPER LIMIT, we can isolate each band of the emission spectrum and calculate how much of each our star outputs.

For Ultraviolet we can plot from X-Ray (0.001µm) to Violet (0.385µm).

For Visible light, close in between 0.385µm and 0.750µm.

For Infrared, go from 0.750µm up to 50µm.

On the side where is written RESULTS, look for RADIANCE, thats the total output of the blackbody, now taking that as 100%, look down and compare with BAND RADIANCE.

The given value is your emission proportion. 

For Vol, we have:

UV = ~11,2%

VIS = ~43,7%

IR =  ~45%

This sum up to 99,2%, we can assume that its missing 0,8% are in the far radio and gamma-ray bands...

OKAY, guess it is up to you now what to do with this information, it literally is a building block for whatever biology you wanna build, if you star supposedly emits way more UV than our Sun in a way that colonists have to wear their vehicles with black-tinted windows and such or your small red dwarf outputs a microwave pulse as a lighthouse because someone had build a dyson sphere around it, ya already know what to look for here...

- M. O. Valent, 10/06/2019