UNIFIED TABLE 2024 UPDATE

One sheet to track them all, one sheet to find them,
One sheet to sort them all, and in the data bind them,
In the depths of space where our worlds lie.

Hello dear visitor. It's been quite a while since I last posted anything on this site (over 9 months), so I thought that I could give you guys a little update on the model I use for all my writing and napkin calculations whenever prompted.

In case some of  you haven't noticed yet, HARD SCI-FI has a little link to a page containing all the calculators and spreadsheets I used for posts throughout the blog's history, it's on the right-side on the PAGES block.

It has been somewhat useful for me to revisit some of these tools from time to time in my creative process, but it can be quite overwhelming at times to open a dozen tabs and make copies of those as to not alter previous work. Back in 2022 I have attempted to summarize all the math used in my WIP guideline book (?), but as of them it was rather incomplete, and as of now it does not reflect my current understanding of its aims and the science of it.

 

Screenshot of the 2022 table, on STARS

So now, until the end 2024 I'll be working on a new table of contents that summarize the math in each of the chapters for ease of use, it will be also be a more consistent model as now the different tables will be able to cross-reference themselves, for a reasonable  approximation of reality as I've come to know it.

Though, I'll likely keep the same  streamlined look and palette to it.

Also, leaving this disclaimer from the opening text from the guide (before anyone comments on it):

Therefore, this work establishes a set of rules for a simplified model of the universe, which, while similar, is not precisely like our own.

- M.O. Valent, 17/10/2024 

BIOLOGY | PART 3 | A BRIEF INTRODUCTION TO EVOLUTION

IMPROVISE. ADAPT. OVERCOME!

Hell yea  E V O L U T I O N, finally we got there, been trying to come up with a consistent creature lineage for months and I and got it, be showing the first ones next post.

So, let's recap some of what evolution is:

- The process by which different kinds of living organisms are thought to have developed and diversified from earlier forms during the history of the Earth.

- The gradual development of something, especially from a simple to a more complex form. 

Nice, then let's fix some misinformation about it:

EVOLUTION HAS A GOAL, AND THUS IT "STOPS" WHEN THE SHAPE IT ACQUIRED IS "PERFECT" / EVOLUTION ONLY WORKS AT TIMES OF CRISIS.

No! It doesn't work like that. Evolution has no specific GOAL body-plan, but to shape it in a way to better suit to it's environment. Any given creature/species keep evolving even at "stable" conditions, crocodiles existed for millions of years and maintained a fairly regular shape, but they haven't stopped evolving, evolution doesn't always express in it's phenotype, ie, the part of the genes that are responsible for external features (crests, eye color, skin color, etc.), evolution continues to happen slower and more internally in a "stable" environment, crocodiles will continue to fight bacteria and viruses and develop resistance against them from generation to generation, rates of reproduction and means of reproduction will still be under miss-copying of DNA codes leading to variation, life works this way, because one day or another these variation ponds will be essential for the survival of the species. When a crisis happen, like rapid-changing climate or vegetation, which may affect a large potion of the gene pond, those changes are clearly more visible and if so happens, individuals will have drastic mutations variants compared to their predecessors, and those will have more chances to survive.

For instance, we have a certain set of bugs which colors range brightly from light green to red, and a storm takes some over to an neighboring island, where birds doesn't see much of red, due lack of red fruits in the area.

Birds will prey on light-green, and yellow bugs, but not much on the orange-red ones. After some generations, the entire species of bug will not "become" red, but rather, the green and yellow phenotypes, or at least the active ones will be long gone, letting only the ones with red coloration. The gene pond will be always there, if by some manipulation of the environment, say by removing any predators, the green and yellow will slowly come back to existence, although in small numbers. Some times in cases like these, the separated group become a totally different species, let's say, if the birds are eating these bugs because they're shaped like peas, then the newer bugs beside red, will also be more elongated like  grains of rice or peanuts so it doesn't fit well in the bird's beak.

There is a good reason why evolution is often misinterpreted this way, it is called Convergent Evolution, when two or more unrelated creatures converge into one similar design, see Dolphins - a mammal, and Sharks - a fish.  This argument also lead many of sci-fi writers and scientists at the early 20th century to discredit H.G. Wells in his book The War of the Worlds, which presents advanced alien invaders as octopus-like creatures with beaks. Those scientists discredited any alien representation under the argument of convergent evolution, that any other alien advanced enough to develop a society should resemble the human body-plan, as that would be some sort of requirement for success as an species.

EVOLUTION IS LINEAR, THE "MARCH OF PROGRESS"

Well, is very common evolution to be depicted by the march of progress:

Probably the first thing that comes to mind when we think of evolution besides dinosaurs and Darwin.

To state a species come right after another like in a domino trail is by far the worst depiction of evolution, and again, it subjectively states evolution has a "goal" body-plan.

An evolution representation that better suits reality and still, very pretty spaced because we can't list every single path, but the significant ones where we able to distinguish with our eyes, it is called a Cladogram.

Where at the base we have the common ancestor of all the above species, each bifurcation is a common ancestor of the upcoming branches, like the first Theropod, that may have resembled a bit of a small velociraptor or coelophysis, but from there begun the branches to the dylophosaur, t-rex, and ultimately, birds.

Some animals been there since the beginning of time, like mammals, we just come to shine in the last 60 or so million years, but mammals and their ancestry been present since the Permian period, 270 million years ago, take as great example, the Dimetrodon, yes it is not a dinosaur, is one of the ancestors of mammals.

And lastly:

EVOLUTION CAN TAKE CRAZY PATHS

Yes, it can, but consistently. You can't have six-legged and four-legged creatures coexisting in the same planet for long, one will eventually outpass one another, all Earth animals (wayyyy general case for non-arthropod) are tetrapods, ie, decends the four-legged ancient salamander.

A head, two superior limbs, two inferior limbs, two eyes, two hearing apparatus and a tail, characteristics inherited from the first tetrapod.

As well, if your planet has been colonized by a hexapod, or octapod, all animals proceeding this common ancestor should have a similar body structure, just re-scaled or lost limbs/parts.

 

Bye!

- M.O. Valent, 03/09/2019

BUILDING BLOCKS | PART 6 | KEPLERIAN DISTRIBUTION

KEPLERIAN DISTRIBUTION...

And I well thought I wouldn't come back to the BUILDING BLOCKS section, ha, I was pretty wrong I guess.

SO, last time we scratched a talk about placing planets in their orbits (PART 4), we saw what I now call 'Keplerian Distribution', in short, you set a base number, usually 0, and build up a progressive sequence with some sum or subtraction over it, and there are your planetary orbits.

If we take a look at our solar system, we will notice how planets are spaced.

Mercury - 0,38 AU

Venus - 0,73 AU

Earth - 1,00 AU 

Mars - 1,52 AU 

Jupiter - 5,2 AU

Saturn - 9,5 AU

- -

Johannes Kepler when measuring the Solar System, noticed that if we begin a sequence at 0, 3, 6, 12, 24, 48, 96... and so on, added 4 and divided by 10.

4, 7, 10, 16, 28, 52, 100... /10  =  0,4 AU, 0,7 AU, 1 AU, 1,6 AU, 2,8 AU, 5,2 AU, 10 AU...

Of course this kinda works well because stable orbits form from orbital resonances, and those really have a progressive mathematical relationship.

The original Keplerian Distribution falls like:

 A = ([0, 3, 6...] + 4) / 10

Repeat the procedure for every planet you have to put in place.

Keep in mind that although I stated C is any given value between 0 and 10, that is not quite a rule, but also, your orbits that fall outside the outer boundary of a star system (forty times the host star mass in AU) must be excluded if so.

I've made a Keplerian Distribution Graph in case you having any problems in visualizing what's going on.

- M.O. Valent, 28/06/2019

OTHER CONCEPTS | SUNSETS

S U N S E T S

HEY! VSAUCE HaSFi! Valent here...

Ever sat at an open field or beach, to watch the sun set?

If no, you should probably do it someday, well I love watching the sunset, not only because I like seeing the stars and satellite constellations fade in, but also, because the sky changes its color as well the sun does...

Sky color...

Rayleigh Scattering is responsible for making our skies and blue eyes BLUE, shorter wavelengths like violet and blue gets scattered more in the particles that make blue eyes and air than longer wavelengths like yellow and red.

Except when during the sunset, there is way more air in the way, so all the blue light coming from the sun scatters in the way, and only the yellows and red photons manage to go practically straight through towards your retina... We see a orange/reddish sun setting...

You can also observe this phenomenon while in pretty polluted urban areas, when the pollution makes the air so dense, that you can actually the see the golden disk of the sun through the smog.

The atmosphere thickness is roughly 100km, being that most of it (97~99%) is concentrated in less than 30km high, during noon you can see the blue sky and an overall white/yellowish sun.

When the sun is setting, there is around 639km of atmosphere in the way, making it reddish, and for that, since yellow/red light are ~45% the visible spectrum, we can assume this much atmosphere is gradually responsible for "absorbing" ~65% of the incoming sunlight, we will come back to this later.

If we make the atmosphere thicker, twice as thick for instance, during noon the sun will appear yellow as during 9h and 15h because of those extra ~30km in the way. As such, during sunset or sunrise, there will be ~816,5km, in this case absorbing up to 83% of the visible spectrum, letting only red and deep red pass by.

Now remember when I said that the atmosphere "absorbs" blue light in the path during sunset?

We can plot how much air is needed for the sun to appear a certain color, this will give us some idea of what is going on.

Okay, so, for an Earth-sized planet and an Earthly atmosphere, we have:

Atmosphere height = 32km (99% atmospheric mass)

50% of AT.mass is located within 5,5km from ground.

40% of AT.mass is located between 5,5km and 18km from ground.

9% is located between 18km and 32km from ground.

1% is spread up 600km high (ignore it)

Then we notice that:

50% AT.mass occupies only 17% of the AT.volume.

40% AT.mass occupies another 54% of the AT.volume.

10% AT.mass is spread across the rest 28% of AT.volume.

And this proportions are valid for any direction you look at in an earth-like atmosphere.

Let's face the atmosphere density as those 3 phases, any direction we look at will pass through these 3 phases, but in different scales, unless you are in higher altitudes, but we are counting for an observer at sea level.

Now, for Earth we have 639,28km of air in the way during sunset, which is ~19,97x thicker than the atmosphere at zenith.

Using triangles and the horizon drop to determine at what distance each phase of atmosphere ends, we see that the phases maintain their proportion, like we said before.

50% of the air in the way stands up only in the first 110km, the other 40% are up to 458km and etc.

 

110km is 20x thicker than 5,5km, hence, we have 20x more absorbency than at noon, we find that at noon, atmosphere filters 3,25% the visible spectrum starting from violet.

If the sun is 45º high, the atmosphere in its direction is 14,14x thicker so its absorbency is 14x than at n--

NOOOO NONONO! Am gonna stop you right there!

See, when we draw our triangle being 32km high (atmosphere height) and 45º in one side, we get our hypotenuse 452,5km long, the path of light is 14x greater than at zenith, BUT when we look at our phase boundaries, they've only grown up by 40%, then the real absorbency is 1,4x the zenith's.

At sunset/sunrise and noon are the only valid straight up values that are true, for any other direction you must divide the hypotenuse length by the atmosphere height which happens to be the opposite side of the triangle.

Now, how do I calculate this for a different planet?

We will need to calculate chords...

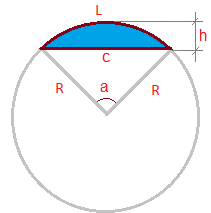
On the picture:

L - arc length

h- height

c- chord

R- radius

a- angle in degrees

But, let's consider 3 things first:

1. We know the radius of our planet (Rp), and we know the height of our atmosphere at the zenith (hA).

2. We know the radius of our atmosphere. (RA= Rp + hA)

3. Height of our chord shouldn't be higher than hA.

Now, let's say our planet is 5.000km radii, and it's atmosphere is 52km high (sun-like star):

Rp = 5.000 km

hA = 52 km

RA = 5.052 km

c = 2 * [ RA * sin( a / 2 ) ]

c = 2 * [ 5.052 * sin( 16,458 / 2 ) ] = 1.446.18 km

Since we can only look one direction at the time (duh) we just need half this segment for our maths... So our useful c' is 723km.

h = RA * [ 1 - cos( 16,456 / 2 )]

h = 5.052 * [ 1 - cos( 16,456 / 2 )]

h = 52,00 km.

For Earth the angle a just happens to be 11,463º.

Okay, so 723km are 13,9x thicker than 52km, and 52km is 1,625x thicker than 32km.

1,625 * 3,25% = 5,28%, is how much light is scattered away during this planet's noon.

13,9 * 5,28% = 73,392%, is how much light is scattered away during this planet's sunset/sunrise.

I will someday find out a real formula for that which will pop the exact ratio of atmosphere in the way, but for now, we have a Desmos graph, and even so, my abilities with it are pretty limited...

This graph is configured for Earth, and I recommend you to have a protractor in hand while calculating your angles... 

[VAL'S ATMOSPHERE THICKNESS GRAPH]

Here is how it works:

Line Code:

Green - Earth's surface

Blue - 5,5km high (Lower Troposphere)

Purple - 18km high (Lower Stratosphere)

Black - 32km high (Stratosphere)

Red - Viewing path

Variables:

c - Any value between 0 and -10 will give an angle between 0º and 90º up. Tweak in between 0 and -1 for angles up to 45º. Check your angle by aligning the protractor with the graph's origin.

r - Planet radius.

b - height of the graph, set it to minus r so your planet surface lies on the origin.

To obtain the atmospheric layers radius, divide it's height* by the planet radii, then subtract it from 1,0. Set the numeric variable in the graphs with the resulting number.

*calculate the heights with the proportions previously stated.

Since your observing point is the origin (0,0), the intersection point between the red line and any atmospheric layer coordinates gives your triangle sides, where the X coord. is the base, and the  Y coord. is the opposite side. Square them up and root the hypotenuse up to get the path.

If your line pass through the (14.4 , 2.4) coordinates (Lower Troposphere), your triangle is 2,4²+14,4² = 14,59². 14,59km is 2,65x 5,5km, then, by looking 9,46º the atmosphere visible light absorbency is 2,65x that of noon.

You can follow like that and so on.

Bye.

- M. O. Valent, 25/06/2019