SCIENCE&ARTWORK | BINARY STAR SUNDIAL | PART 2

WHAT ABOUT DIFFERENT STARS?

So excited Nyrath from Atomic Rockets shared my last post! LETSGOOO

A few reddit users pointed out if the bisolar clock I designed assumes that both stars are the same mass, thus orbiting a common center of mass equally spaced between them, here is why I made this initial assumption while working on the model:

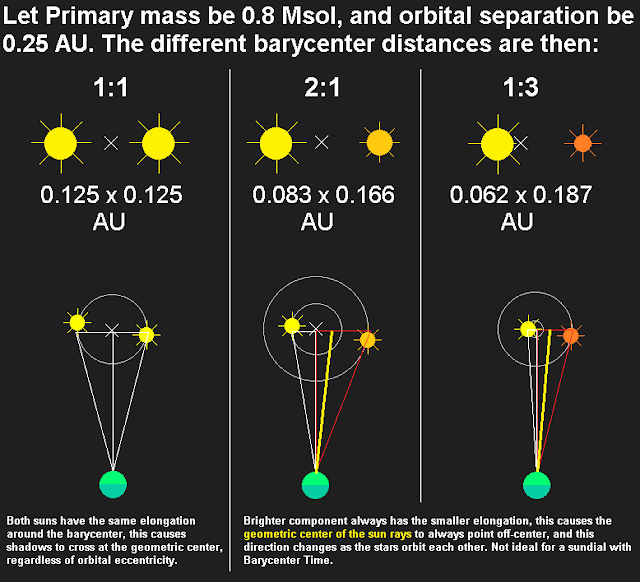
So as you can see, we've got a bit of a problem here, not only with getting the instant time of the day when the two stars are not of similar mass, but also getting the time at any point in their orbital period, since this geometric center would wobble back and forth.

However, the greater the mass difference, the greater the difference in luminous output from the stars, so in a way - the greater mass difference would make the secondary component less relevant for the clock building.

1.0 Msol ~ 1.00 Lsol

0.8 Msol ~ 0.50 Lsol

0.5 Msol ~ 0.10 Lsol

0.2 Msol ~ 0.01 Lsol

and so on...

So with greater mass difference, unless we're dealing with massive stars like F or A-types, the less relevant the secondary component becomes, but luminosity follows roughly the cube root of the stellar mass, which means that although the luminosity from the secondary isn't as influential, its mass still is. That dim star would still make the brighter component wobble.

From the given examples above, the 1:2 system has an orbital period of 41.17 days, and the 3:1 of 43.66 days - the 1:1 system is the same as the previous post. The secondary in each of the two examples has luminosity as 0.06 and 0.02 Lsol, quite insignificant for any clock building purposes, as the primary is about 10x as luminous.

Since both systems have similar luminosity, I will set up our observer planet at 0.75 AU for both. The maximum elongation of the primary is then 6.35° for the 1:2 case, and 4.74° for the 1:3 case.

If we keep the 36 hour day, that means our clocks may be up to 38 and 28 minutes ahead/behind barycenter time. And since this difference develops slowly over the course of some...

1:2 case ~ 50.97 days, planet year is 213.8904 Earth-days,

1:3 case ~ 54.32 days, planet year is 226.8933 Earth-days,

We can just add those variations to the equation of time, by adding a sine wave with the equivalent time difference amplitude and synodic period of the stars. I'll use 20° axial tilt and 0.01675 eccentricity for the EoT generation.

1:2 case

1:3 case

Given this solution, any ordinary Earth sundial works in such world, for as long you consider this modified equation of time for your planet, just look for the darker shadow whenever checking the time.

KEEPING TIME AROUND AN 8-SHAPED ORBIT???

Another user spoke about a project they have involving a planet with a 8-shaped orbit around its two parent stars, with a pretty usual set of circumbinary planets after it.

Now, since it is not the goal of the project to be 100% Interstelar-level physics plus some magic dust sprinkled on top, I'm not getting into how to plan those orbits, or how no planets could form under such conditions, let's just exercise and have fun, because some realities are just sad.

You might also want to look into Arenstorf Orbits - those can be pretty dope and are used for planned satellite missions. About the 1 year period, I'm rather unsure if that's possible at all without having the stars several AU apart (and the planet freezing midway to the other pair), the proximity to the stars and orbital speed necessary for orbital transfer inside the gravity well of whole stars would mean that the planet likely going to complete the circuit in a few days or even hours, in what it is called a Free Return trajectory.

In this situation, no conventional methods for time keeping work, because sundials work on the regular passage of the sun, and it gets even worse if one actually opts of an Arenstorf-like orbit, where you've got many loops of different sizes. Given that, it seems more efficient to track the time at night, when the stars are visible - if the planet rotation happens within reasonable fraction of the planet orbital period, say like, within 7 local days, or if the planet somehow rotates at such speed that a single hemisphere always faces forward in the orbit, and the other trails behind.

At different points of the orbit, the night/dark sections of the planet would point towards different constellations of the local zodiac, ex; some constellations appear on the east only if you're approaching the smaller stars, while the same constellation appears on the west as you leave that star - because the planet is now facing the other direction.

As the stars orbit each other over a period of less than 100 days, those constellations would change as well (given sun-like stars at < 1.0 AU), returning as they were after some 3 months. Plus, given the planet rotation being similar or even longer than its orbital period, we get some trippy sun movements, I suppose even more confusing around two stars.

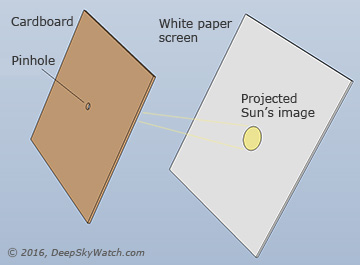
For timekeeping during the day, there is one simple scheme I propose, a pinhole projection clock!

As the planet races from one star to another, the apparent size of the stars in the sky changes, and a safe way to measure this is through a pinhole projection, since the projection size is always proportional to the object's true size in relation to its distance from the observer.

R/D = r/d

Where R is the real diameter and D the real distance, and the r is the projected diameter and d the distance between pinhole and screen.

By tracing concentric circles of different sizes inside the box, one can know the precise time in terms of the planet's trajectory around the suns - like quarter, half-way, and maximum diameter for one or both stars, and all you have to do is to point the box and look inside through a lateral aperture. People have used a very similar setup to watch solar eclipses here on Earth.

With the invention of glass and lenswork, a more compact and sophisticated method can be used, using a small telescope or lens to project onto a small screen (I imagine such an instrument would be size of a toothpaste box), and the same concentric circles inscribed in the screen would serve to tell the time down to the day.

UNTIL ANOTHER DAY!

- M.O. Valent, 09/03/2023