SCIENCE&ARTWORK | BINARY STAR SUNDIAL | PART 2

WHAT ABOUT DIFFERENT STARS?

So excited Nyrath from Atomic Rockets shared my last post! LETSGOOO

A few reddit users pointed out if the bisolar clock I designed assumes that both stars are the same mass, thus orbiting a common center of mass equally spaced between them, here is why I made this initial assumption while working on the model:

So as you can see, we've got a bit of a problem here, not only with getting the instant time of the day when the two stars are not of similar mass, but also getting the time at any point in their orbital period, since this geometric center would wobble back and forth.

However, the greater the mass difference, the greater the difference in luminous output from the stars, so in a way - the greater mass difference would make the secondary component less relevant for the clock building.

1.0 Msol ~ 1.00 Lsol

0.8 Msol ~ 0.50 Lsol

0.5 Msol ~ 0.10 Lsol

0.2 Msol ~ 0.01 Lsol

and so on...

So with greater mass difference, unless we're dealing with massive stars like F or A-types, the less relevant the secondary component becomes, but luminosity follows roughly the cube root of the stellar mass, which means that although the luminosity from the secondary isn't as influential, its mass still is. That dim star would still make the brighter component wobble.

From the given examples above, the 1:2 system has an orbital period of 41.17 days, and the 3:1 of 43.66 days - the 1:1 system is the same as the previous post. The secondary in each of the two examples has luminosity as 0.06 and 0.02 Lsol, quite insignificant for any clock building purposes, as the primary is about 10x as luminous.

Since both systems have similar luminosity, I will set up our observer planet at 0.75 AU for both. The maximum elongation of the primary is then 6.35° for the 1:2 case, and 4.74° for the 1:3 case.

If we keep the 36 hour day, that means our clocks may be up to 38 and 28 minutes ahead/behind barycenter time. And since this difference develops slowly over the course of some...

1:2 case ~ 50.97 days, planet year is 213.8904 Earth-days,

1:3 case ~ 54.32 days, planet year is 226.8933 Earth-days,

We can just add those variations to the equation of time, by adding a sine wave with the equivalent time difference amplitude and synodic period of the stars. I'll use 20° axial tilt and 0.01675 eccentricity for the EoT generation.

1:2 case

1:3 case

Given this solution, any ordinary Earth sundial works in such world, for as long you consider this modified equation of time for your planet, just look for the darker shadow whenever checking the time.

KEEPING TIME AROUND AN 8-SHAPED ORBIT???

Another user spoke about a project they have involving a planet with a 8-shaped orbit around its two parent stars, with a pretty usual set of circumbinary planets after it.

Now, since it is not the goal of the project to be 100% Interstelar-level physics plus some magic dust sprinkled on top, I'm not getting into how to plan those orbits, or how no planets could form under such conditions, let's just exercise and have fun, because some realities are just sad.

You might also want to look into Arenstorf Orbits - those can be pretty dope and are used for planned satellite missions. About the 1 year period, I'm rather unsure if that's possible at all without having the stars several AU apart (and the planet freezing midway to the other pair), the proximity to the stars and orbital speed necessary for orbital transfer inside the gravity well of whole stars would mean that the planet likely going to complete the circuit in a few days or even hours, in what it is called a Free Return trajectory.

In this situation, no conventional methods for time keeping work, because sundials work on the regular passage of the sun, and it gets even worse if one actually opts of an Arenstorf-like orbit, where you've got many loops of different sizes. Given that, it seems more efficient to track the time at night, when the stars are visible - if the planet rotation happens within reasonable fraction of the planet orbital period, say like, within 7 local days, or if the planet somehow rotates at such speed that a single hemisphere always faces forward in the orbit, and the other trails behind.

At different points of the orbit, the night/dark sections of the planet would point towards different constellations of the local zodiac, ex; some constellations appear on the east only if you're approaching the smaller stars, while the same constellation appears on the west as you leave that star - because the planet is now facing the other direction.

As the stars orbit each other over a period of less than 100 days, those constellations would change as well (given sun-like stars at < 1.0 AU), returning as they were after some 3 months. Plus, given the planet rotation being similar or even longer than its orbital period, we get some trippy sun movements, I suppose even more confusing around two stars.

For timekeeping during the day, there is one simple scheme I propose, a pinhole projection clock!

As the planet races from one star to another, the apparent size of the stars in the sky changes, and a safe way to measure this is through a pinhole projection, since the projection size is always proportional to the object's true size in relation to its distance from the observer.

R/D = r/d

Where R is the real diameter and D the real distance, and the r is the projected diameter and d the distance between pinhole and screen.

By tracing concentric circles of different sizes inside the box, one can know the precise time in terms of the planet's trajectory around the suns - like quarter, half-way, and maximum diameter for one or both stars, and all you have to do is to point the box and look inside through a lateral aperture. People have used a very similar setup to watch solar eclipses here on Earth.

With the invention of glass and lenswork, a more compact and sophisticated method can be used, using a small telescope or lens to project onto a small screen (I imagine such an instrument would be size of a toothpaste box), and the same concentric circles inscribed in the screen would serve to tell the time down to the day.

UNTIL ANOTHER DAY!

- M.O. Valent, 09/03/2023

SCIENCE&ARTWORK | BINARY STAR SUNDIAL | PART 1

IS IT POSSIBLE TO CONSTRUCT A BINARY STAR's SUNDIAL?

WHY?

So this last week I've been trying to work on my own sundial to settle up an argument (with a flatearther, ugh), It works pretty nicely and got bit damaged by rain since it is made of paper, but my brief study of Gnomonics got me pretty interested in the craft as a whole, there are 'easy' and 'hard' ways to make sundials and solar calendars. You can scroll right to the end if you're not interested in the whole thought process behind its end design.

My first print of my gnomonic sundial, the lines are created by projecting a spherical grid onto a plane which is the dial plate. 

Anyone can use a base and a stick to simply mark the hours by the gnomon's shadow, but the instrument will only be able to tell hours. But to be able to tell the day and months/seasons, the designs and matemathics get a little bit more complex.

Fellas over the northern hemisphere might already be familiarized by the sundial design above, formed by a disk or dial plate, with a triangular gnomon on top of it. None of the shapes here are of arbitrary dimensions, the inclination angle of the gnonmon has to match your Latitude (North/South coordinate), and the size of the gnomon in relation to the plate will determine wether the instrument can only tell hours or include the seasons/month markings. For the northern hemisphere inhabitants, one can eyeball the inclination of the gnomon by pointing to Polaris, the North Star, whereas southern people have to use known landmarks and constellations to get a sense of where to point it.

If you look at my design, you will notice a straight line, and two opposing hyperbolae, the straight line is called the Line of Equinoxes, it is where the shadow of the gnonomon falls during the Autumn and Vernal equinox days (Equinox or Equinoctis meaning "equal nights") - the two opposing hyperbolae are the Solstice lines, where the shadow falls during the summer and winter soltices respectively, by marking intermediary hyperbolae one can mark the passsages of months and weeks through the solar cycle.

Because of the Earth's tilt, one can draft a simple grid like the one I did by constructing a spherical grid marked 23.5° north and south of the equator, then putting a light source at its center, then tilting said spherical grid to the user's latitude - the resulting projection onto a sheet of paper will be your markings, and the distance from the paper to the center of the sphere is the same from the plate to your gnomon's tip, which is what you can see I rendered in the 3D software, then printed.

Without a 3D grid (physical or virtual), it takes a lot of math to traditionally work out the specific lines you'll need for you sundial, that's why the ancients often cut the middle-man and just projected their sundials onto convex hemispheres and rings!

There is a whole bunch of other types of sundials each specific to what their projectionists wanted to be told by the sun as well, but do any of those work for a world with two suns?

THE SETTING

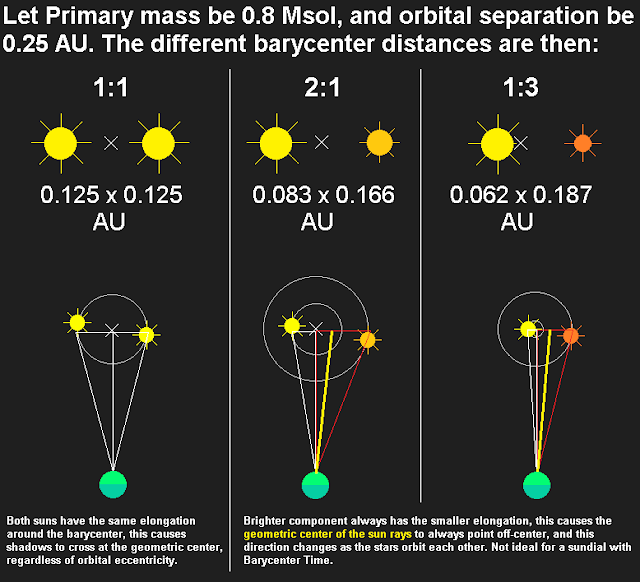
The system's stats I will be using thoughout this post

First of all, a quick googling of "Binary Star Sundial" retrieves not a lot of material, if someone has ever worked on anything like that, they didn't publish it on the internet, there are a couple posts on stackexchange and reddit dating back to 2016 but no solutions, most of them assume you can get away with a normal sundial since the shadows created onto a circumbinary planet would mostly be off by about 10° maximum - but this would only work as an approximation, depending on the specifics of the system, this would mean the clock could be offset by about 1h of the actual time (assuming the planet has 24h day/night cycle).

So before tackling the problem as a whole, let's see what changes from the traditional Terran sundial, so we can better know what challenges lie ahead:

DIFFERENCES BETWEEN SOLAR AND BISOLAR CLOCKS

1. MOVING SUNS

In the traditional solar clock, one can assume an inertial reference point, that could be either the static Earth with the Sun moving around it, or the static Sun-Earth system, with the Earth rotating around its axis.

On a bisolar clock, we have to consider not only either of those scenarios, but also that the suns are not static in the sky, they revolve around a common center of mass. Which means that for either scenario, the suns would always move significantly on a day to day basis - what would in itself, create a solar subcycle our natives to work with.

2. MISALIGNED ECLIPTIC

On Earth, the Ecliptic plane is the apparent path of the Sun across the sky throughout the year, it is pretty easy to follow through and it is what defines the constellations of the zodiac. On a circumbinary system however, one could either define the ecliptic as the planet's orbital plane, or the star's own orbital plane, in either case, both stars would constantly fall above and below the ecliptic as they orbit each other. Which means that the difference in orbital inclination between the stars and observer planet would change throughout the year as well. Anyone familiar with tracking the movements of Mercury and Venus in the sky will known how crazy the paths can look.

Because all of those movements are specific to the times and cycles at play, I will outline my process with an example so you can work out your own models of bisolar clocks. Since we cannot experience such a place, I will be using 3D software to simulate what it should look like based on the model stats given in my sketch.

UNDERSTANDING THE SKY

To keep things simple, I will work with geocentric coordinates, swapped the Sun in the solar system by a pair of twin stars with 80% of the mass, just so the brightness matches just the same on our planet, which had its tilt reduced to 20°. The star's also orbit each other at an angle of 5° from the planet's orbit.

Although for an external observer, the twin suns orbit each other every 36.1 days, the planet which is also orbiting the stars do not perceive this as being 36 Earth-days, we need to calculate the synodic period of the stars by using:

Which works out to be 41.25 Earth-days, or 990 hours, now we can use this information to set up the planet's rotation into some neat value that's easier to work with.

I will set the planet's rotational period to about 36 hours, this gives us a simple 10° per hour rotation, it approaches the solar subcycle to roughly 27.5 sidereal days (similar to a lunar month) - and makes the year about 192½ days. Meaning our stars move 13.1° over the course of a day, and half as much during daytime.

corrected suns declination at +0.624°

Usually, the planet's tropics would be located at latitudes 20° North and South of the Equator, but because the suns can gain about 0.62° of declination along their orbit, we can say that the tropics are found between 19° and 21° from the equator. This means that depending on the suns-planet alignment, the extra declination can come during solar opposition (suns seem aligned) or during maximum elongation (suns seem further apart).

The maximum elongation or separation between the suns in the sky would be about 14.5°, and this gives us another interesting alternative to measure the solar day, Mean Solar Time, which is measured from the barycenter, considered static while the suns orbit around it.

Further refinements put the sidereal day at 35h52m33s for a perfect 36 hour solar day

Let's also start our year in a point in the orbit when the suns seem further apart.

DESIGNING THE HOROLOGIUM BISOLARII

PRELIMINAR EXPERIMENT

An anallematic sundial consists of a vertical gnonom which marks the time throughout the day, but also tracks the months through the solar anallema by the length of the gnomon's shadow.

On Bisolaria, such an anallematic clock would produce two shadows which dance with twice the speed of the suns orbital period.

Each square is 10cm wide for scale, and the gnomon has 10cm from the base to the center of the sphere, the star light was tinted yellow and blue to differentiate, each time they switch sides corresponds to half a solar subcycle, and the whole animation takes place over two years (~385 sidereal days) on this planet, Bisolaria.

Each frame in the animation is taken at exact mean solar noon - if we picked a star to count solar days, then the frame of reference would wobble back&forth across all the four cardinal directions as that sun moves across the sky throughout the year, undesirable, which is why we count from the barycenter. Here we can also see the effects of the star's orbital inclination, at times a shadow appears longer than the other by a noticeable amount.

I bet we can use that tilt in the stellar orbital plane and the fact we are working with two shadows to come up with a creative horizontal anallematic clock and calendar. Why not double down with two gnomons then? My initial idea is to use two longer gnomons spaced in such a way that their shadows cross most of the time, the line at which they cross would determine the time of the year, while the point at which they cross would make up for the current hour of the day.

LOOKING AT THE SKY

So throughout the years, we would see the suns eclipse each other only during the planet's passage through the nodal line, where the sun plane crosses the ecliptic plane. We would also see the sun plane appear to tilt north or south as we cross the south and north pointing sides of the orbit, which by itself would be a good teller of seasons.

But we also have to consider the effects of the planet's orbital eccentricity, because the planet moves faster around the suns when it's closer than when it is farther - this causes the mean solar time to go faster and slower than the planet's true rotation period by a few minutes, which is what the Equation of Time is about.

I'm not mentally stable nor know math enough to digest the needed equations so I could explain them better, but I've found a couple tools online that will be useful in generating the data require to produce a clock for a fictional world:

• Analemma Calculator
• Sage Cell - Equation of Time

While the Analemma Calculator is pretty straightforward with single-sun systems, we'd need more work for the paths of the two or more suns we include. Below is a generalized version of the SageCell code, pointing where you need to input your data - if you're not familiar with Earth's parameters.

NON-FICTION | THE ONLY UFO THEORY I'M NOT SO SKEPTICAL OF

 DO I WANT TO BELIEVE?

    

Okay, I know that my typical content is centered around Sci-Fi and fun thought experiments, but this morning I had a revelation of sorts, actually I discussed this with brother a few times before. Every now and then I ask him about how's his view on alien life and we end up chatting for about an hour. But today we connected some dots I don't think anyone has done before.

Before anything, allow me to clarify what's my position regarding Ufology as a science: I don't think most of the reasearch should be taken seriously, for real. There is no scientific approach and the theories are often too out of this world with no regard for astrophysics and astronomy, as I have said across various posts. It is very easy to be an adept of the UFO research movement when you can simply say they have advanced tech that's research-proof about anything you try to explain, it fails the falsifiability test and becomes pseudo-science, which leads me to think most of it doesn't deserve attention and funding. Add that to UFO groups in Brazil refusing to speak to me when asked a few questions like those I present in this blog.

Falsifiability, is the capacity for some proposition, statement, theory or hypothesis to be proven wrong.

SO WHAT CHANGED NOW?

If it is not clear by now, I really think most of UFO research should not be taken seriously because there is apparently, lack of any physical thrustworthy evidence of any claims, but a lack of methods to investigate so. Because of that, anything could be explained with enough skepticism with natural phenomena and with a simple "I don't really know". And I say 'apparently' because a few years ago the US government released some official footage of UFO chases in 2020, or as they like to put it up 'unexplained aerial phenomena', and this kind of thing suddenly turns out too dangerously real. Not to speak of rumors to recent Blue Book project re-opening.

I used to make fun of these movements, and I think I still will until proven otherwise with strong evidence. "Why would aliens come down from light-years away to kidnap cows and probe a redneck's anus?". Yeah, but even in my sketch of a theory, that ends up making a vital part of it, in such a way to not make it as ridiculous as it initially sounds. So here we go.

THE ALIENS ARE STRANDED IN THE SOLAR SYSTEM

Like any other UFO theory, this was made into a logical narrative the takes the premise of alien visitors being real, but from my line of thought, in a more realistic and bland view of things.

This theory also proposes a possible solution to the Fermi Paradox in a way, as in that interstellar travel must be very hard, even with advanced technology, and that no civilizations post Kardashev 1-2 inhabit our local space of the Milky Way, as far as we can tell.

The great silence could be explained with technological civilizations being relatively recent, with some barely older or younger than us by a few thousand years, but not incredibly old, else their technosignatures would be screaming in the sky. In this case such technosignatures are more faint than we initially expect them to be, as in that you don't really need a dyson sphere or to turn your planet into an ecumenopolis to really show you're advanced. It could also be that superluminal travel is possible at very high costs, but no superluminal communication. Since the we are the ones being visited, it is logical to assume we are relatively young compared to our visitor civilization, and yes singular, there is likely only one race trying to contact us in this scenario.

VARGINHA AND ROSWELL INCIDENTS

The Roswell Incident (1947) doens't require much presentation, but I wanna drag your attention to its less known counterpart, the Varginha Incident (1996). Much like the american incident, there was heavy military involvement, and attempts to keep curious and civilians away from the case, and apart from the movie stereotype of aliens arriving to speak to the president of the US, it happened in a third world country with no spectacle, and several civilizan witnesses with no previous history of such events in the very interior of Brazil, too serious to be ignored.   

I'm pretty inclined to believe that the image of the typical Grey alien is cultural inheritance from illustrations of HG WELLS 'Man from the Year Million', but suspending some skepticism off of it, that is, taking the sightings to be true events, one has to consider if it makes any sense in real life...

Now, how come the part where you ask me, "but Valent, the two aliens are so different, how come you say they belong to the same race? There must be more than one visitor race". Come on, this is no star trek where you can get out of your ship and simply kiss your alien girlfriend, in the real world, every other environment but your native one will be hostile for your organism, I don't believe I am the first one to say this, but, you guys really think aliens be roaming the galaxy naked? They must be using some kind of space suit of some sort which allows them to survive in our atmosphere, not because it is toxic, but because of possible pathogens, at least in most cases. People like to interpret the alien drawings as being fully organic naked weirdos putting probes up your ass, completely exposed to contamination hazards.

So yea, let's consider we don't truly know what these aliens ACTUALLY look like, because they have spacesuits on, pretty much like how the Engineers in the Alien universe seem to have a trunk, but is only a mask and they actually look like some albino guy.

The sketches of aliens that depict these guys as fully organic and naked cannot be trusted, since the features or lack of any special features can indicate a type of suit, say like the "horns" in the Varginha alien, they could be tubes or flashlights atop of a helmet of some sort. Given how Greys and the Varginha alien are similar in size and time period, I will cut this down with Ockhan's razor and reduce our visitors to one single group of aliens. After all, what are the chances we've been visited multiple times by multiple races and still live in the Great Silence?

Their spacecraft, at least the ones we've seen so far, aren't indestructible, as we have supposedly taken down a few of them over the years. The overall shape of their vehicles is the bus or tic-tac shaped object, again, what leads me to think it may be the same kind of vehicle or similar every time.

And instead of only calling them aliens from this point foward, and for the sake of cool, I will refer to these as the V-race (get it? several references at once).

The idea is that despite our brutality and lack of understanding, they do comprehend to an extent what we are going through, and have been observing us for a few centuries, and trying eventual contact since the mid 20th century, as we have started to become more technological and exploring space. Yes you heard it right, observing us for centuries.

THE CONSPIRACY TIMELINE

You guys remember the black object that interacted with the Sun back in 2012? Here's official footage in case you doubt it is real. And here it appears again in 2018, and here is a report of it appearing again for 8 days during last month. How long has this object been around? How long have we been really watching the Sun to look for it? I know many artifacts and errors can occur in instruments and this could be diagnosed as such, maybe, somehow, but what if it doesn't? Should we expect the huge 10 Earth-radius object to appear again in the following years? In my opinion, we won't see it again after 2030-2040.

I think this black orb is what astronomers of previous centuries called planet 'Vulcan'. Back in 1611 there were observations of objects in front of the sun, later dismissed as solar spots. Which is quite probable, since they cycle every 11 years, and the early 1600s were marked by a peak of sunspot activity, these can get so large as to equal the size of Jupiter.

The theory of planet Vulcan really took off in the 1800s, when again, two objects were seen crossing the sun's disk through telescope, although the objects seen between 1818 and 1837 were much smaller, if you assume a distance of 100 million km from Earth (close to the Sun), the size of the larger object is around 1500 km wide, half the size of our Moon.

Le Verrier failed every attempt to explain Mercury's orbital precession through the existence of Vulcan, even though he could do the same with Neptune using Newtonian gravity. Nowadays it is explained through Einstein's Relativity on how the sun warps the space in order to cause Mercury to behave like that, and the math checks out so far.

These sightings also occurred before great sunspot events later that year or on the following years, this includes the 2012, 2018, and 2022 sightings, with possible oncoming sightings in 2024-2026 and 2030-2032.

Couldn't it be just sunspots? OF COURSE, but what's the fun in that? Plus, while the observed objects in 1600s and 1800s were passing in front of the sun, the giant orb appears next to the sun, and it would be too obvious if it somehow passed in front of the sun. If it is maneuverable, then it is forcing itself to not pass in front of the sun in respect to Earth. And here we go, failing the falsifiability test, like other theories of the kind.

The V-race has been observing us for at least some 400 years, and attempting peaceful contact since the 1900s, they are not vastly superior than humanity, it may even be their first ever attempt at first contact, taking for the catastrophic incidents of Roswell and Varginha, or at least, they lack the authorization or equipment to do so at the current time. But their home world might be way more advanced than they are because of isolation.

I cannot help but laugh and be slightly worried by what train of thought this is.

If the massive object we've seen recently is real, consider it being like a submarine, weighing less than 1 ton per cubic meter, and its mass can be as low as that of Saturn (~100 Earth-masses), which is a problem yet to solve with this theory. One possible explanation to what it is doing with the sun, is star lifting. It could explain the origin of the materials and energy used by their equipment, needing to approach the Sun every ~200 years for refueling. They haven't left our system since, or if they have so, they somehow can do it without leaving any radiation signatures or from the other side of the Sun, hiding themselves from us.

But I'm inclined to the version they are stranded and receiving orders slowly because of how badly they have been received on Earth, they may be lacking personel, morale, or and may be simply clueless on how to establish proper dialogue with us hairless apes. And on the possibility of them being stranded, it would explain why they land in rural and wild areas, not only to research the local fauna and flora, but to identify what's realistically edible on Earth that they could sustain on, this vary from humans, wildlife, and cattle, yes, pretty much abducting cows for meat, and grain for flour, with enough samples they could start their own space farming - the Earth is so vast they could be around antarctic ice collecting water as well to sustain their crew stationed near the sun or opposite to Earth on the other side.

That's what I have for now...

- M.O. Valent, 05/10/2022